贝塞尔曲线的产生与一个汽车品牌——雪铁龙有关。雪铁龙是法国汽车品牌，由安德烈·雪铁龙于1919年创立。

1959年，雪铁龙的物理学家和数学家Paul de Casteljau运用de Casteljau算法，以稳定数值的方法求出贝塞尔曲线。

1962年，雪铁龙的工程师Pierre Bézier（皮埃尔·贝塞尔），运用贝塞尔曲线来为汽车的主体进行设计，发表了大量的文章，进行了广泛的宣传。

贝塞尔曲线是一种平滑的曲线，并且贝塞尔曲线是一系列的曲线，变化多端。

贝塞尔曲线经常用在计算机图形学中。 比如我们在PS或者Sketch里面都有的钢笔工具，在这些绘图工具中，我们可以用钢笔工具绘制出任意形状的带有平滑曲边的形状。

贝塞尔曲线用在动画的变化率上，让动画过程非常的流畅而不突兀， 在CSS3中增加的transition-timing-function属性和animation-timing-function属性都是利用了贝塞尔曲线实现的。

我们在Android、iOS开发中也经常要使用贝塞尔曲线绘制图形和实现动画效果， 比如拉皮筋的效果，下拉刷新、上拉加载更多，放手后的一些动画效果、水波纹动画等。

参考

贝塞尔曲线的绘制，通常使用de Casteljau算法

绘制贝塞尔曲线的动画演示

贝塞尔曲线的数学基础是早在1912年就广为人知的伯恩斯坦多项式。

一阶贝塞尔曲线就是一条直线。

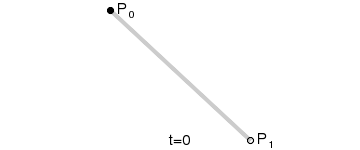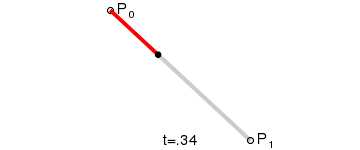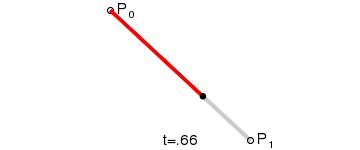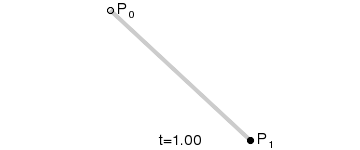
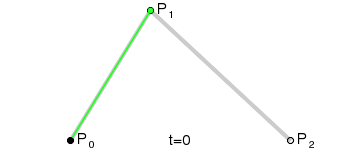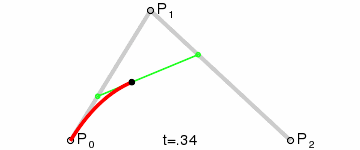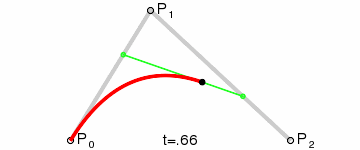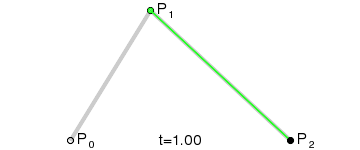
1、在平面内随意选3个不共线的点，依次用线段连接：

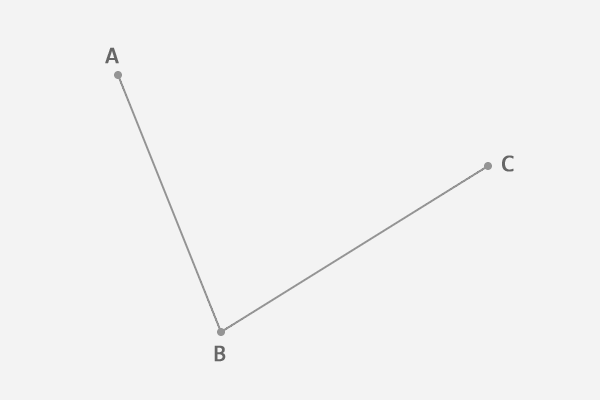
2、在第一条线段上任选一个点D。计算该点到线段起点的距离AD，与该线段总长AB的比例：

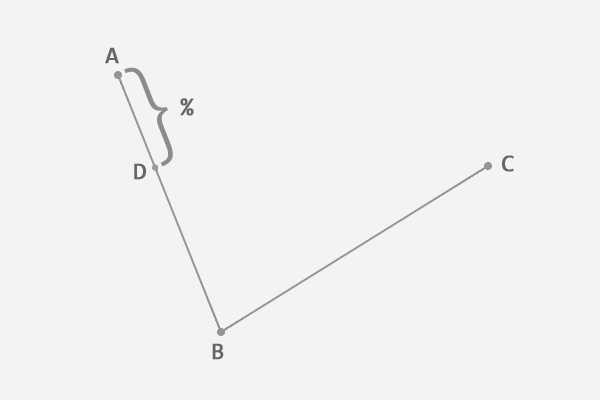
3、从第二条线段上找出对应的点E，使得AD:AB = BE:BC：

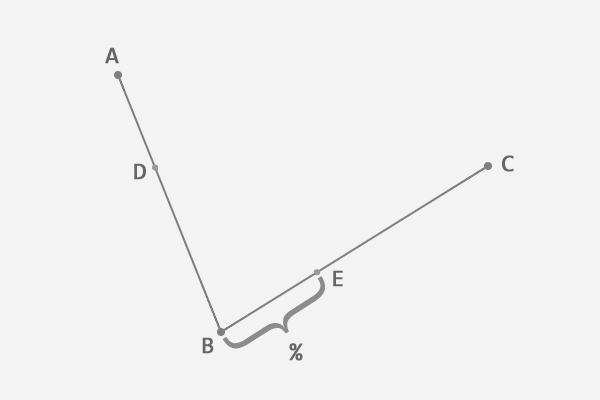
4、连接这两点DE：

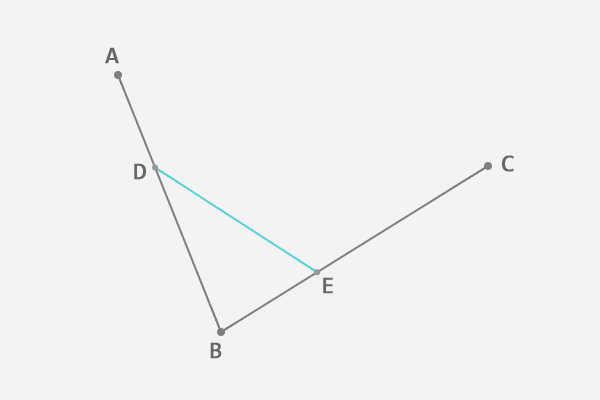
5、从DE上找出点F，使得DF:DE = AD:AB = BE:BC：

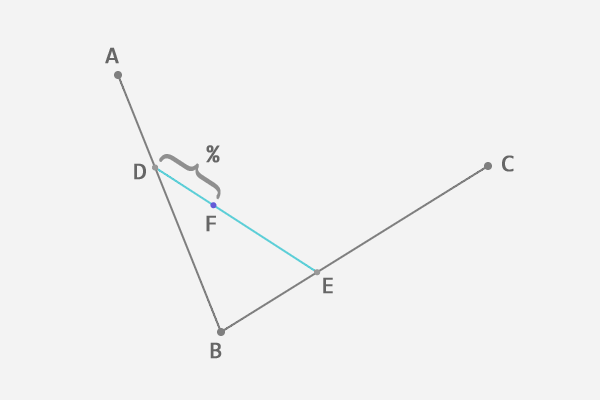
到这里，我们就确定了贝塞尔曲线上的一个点F。为了找到所有的点， 让选取的点D在第一条线段上从起点A移动到终点B，找出所有的贝塞尔曲线上的点F。 所有的点找出来之后，我们也得到了这条贝塞尔曲线：

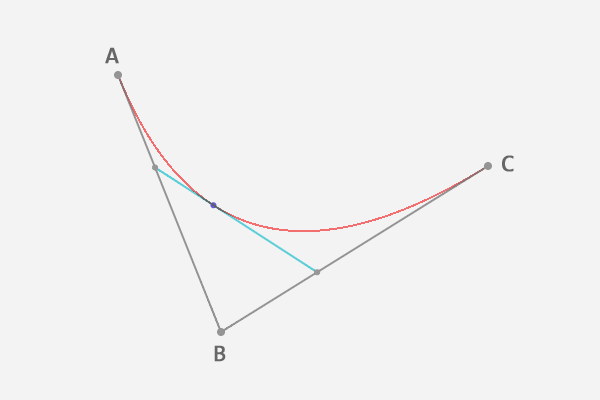
下面是这条贝塞尔曲线的动画过程：

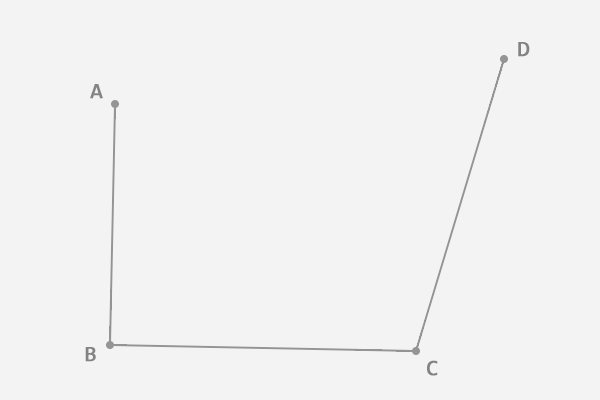
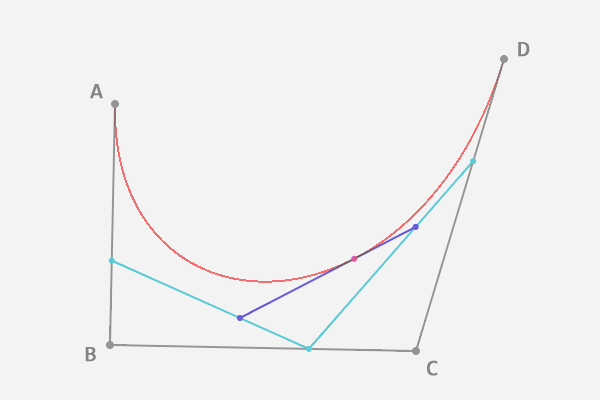
1、在平面内随意选4个不共线的点，依次用线段连接：

2、接下来的操作步骤与二阶贝塞尔曲线的找点是完全相同的，只不过我们每确定一个贝塞尔曲线上的点，要进行三轮取点操作。 如图，AE:AB = BF:BC = CG:CD = EH:EF = FI:FG = HJ:HI，其中点J就是最终得到的贝塞尔曲线上的一个点：

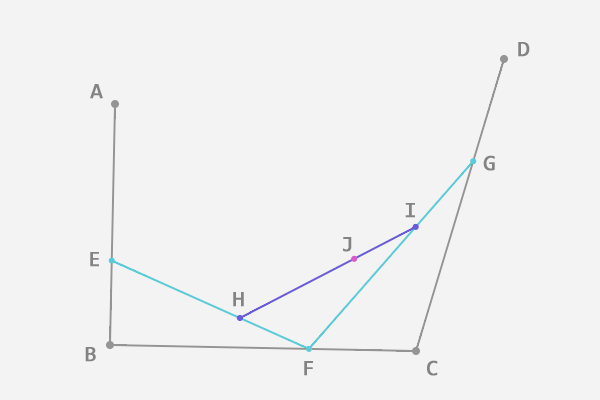
3、为了找到所有的点， 让选取的点E在第一条线段上从起点A移动到终点B，找出所有的贝塞尔曲线上的点J。 所有的点找出来之后，我们也得到了这条贝塞尔曲线：

能画曲线也能画直线；要绘制更复杂的曲线，控制点的增加也仅仅是线性的，这一特点使其不光在工业设计领域大展拳脚， 就连数学基础不好的人也可以比较容易地掌握，比如大多数平面美术设计师们。

推广到三维空间的贝塞尔曲面，以及更进一步的非均匀有理B样条（NURBS），早已成为当今计算机辅助设计（CAD）的行业标准， 不论是我们平常用到的各种产品，还是在电影院看到的精彩大片，都少不了它们的功劳。

Android Framework从一开始就提供了贝塞尔曲线的画法， 只是隐藏在Path.quadTo()和Path.cubicTo()方法中。Path.quadTo()是绘制二阶贝塞尔曲线，Path.cubicTo()是绘制三阶贝塞尔曲线。

SVG有个path标签，可以绘制任意的路径，自然也包括贝塞尔曲线。

示例：

<svg width="190px" height="160px">
  <path d="M10 10 C 20 20, 40 20, 50 10" stroke="3" fill="none"/>
  <path d="M70 10 C 70 20, 120 20, 120 10" stroke="3" fill="none"/>
  <path d="M130 10 C 120 20, 180 20, 170 10" stroke="3" fill="none"/>
  <path d="M10 60 C 20 80, 40 80, 50 60" stroke="3" fill="none"/>
  <path d="M70 60 C 70 80, 110 80, 110 60" stroke="3" fill="none"/>
  <path d="M130 60 C 120 80, 180 80, 170 60" stroke="3" fill="none"/>
  <path d="M10 110 C 20 140, 40 140, 50 110" stroke="3" fill="none"/>
  <path d="M70 110 C 70 140, 110 140, 110 110" stroke="3" fill="none"/>
  <path d="M130 110 C 120 140, 180 140, 170 110" stroke="3" fill="none"/>
</svg>

三阶贝塞尔曲线指令：Mx0 y0 C x1 y1, x2 y2, x3 y3

字母M表示特定动作moveTo, 指将绘图的起点移动到(x0,y0)；

字母C表示特定动作与行为，这里需要大写，表示标准三次方贝塞尔曲线。(x1,y1)和(x2,y2)是两个控制点，(x3,y3)代表曲线的终点。

Canvas有个bezierCurveTo(x1,y1,x2,y2,x3,y3)方法，专门用来绘制三阶贝塞尔曲线的。(x1,y1)、(x2,y2)是两个控制点，(x3,y3)是终点。 起点通过Canvas的moveTo(x0,y0)进行设置。

示例：

var canvas = document.getElementById("canvas-1").getContext("2d");
canvas.beginPath();
canvas.moveTo(20,20);
canvas.bezierCurveTo(20,100,200,100,200,20);
canvas.stroke();

1.6.3.3、贝塞尔曲线与CSS3中的transition-timing-function属性